Finer measures of P1 at Giza
Petrie confirmed that the
smooth angular base casing stones of P1 were carved on a 51.85 degrees angle producing
a ratio equal to 4/pi and resulting in a calculated height of 280.1 Rc. The
apex of the structure was never completed, however, at the upper level Petrie’s
measures produce a completely different picture. The pyramid is actually built
on a 5/4 ratio producing a calculated height lower than first estimated (275
Rc)!
Petrie realized and queried
this ratio but overlooked the possibility of the pyramid built on an angle
different than first assumed by he and his peers. This new angle would
contradict the theory of the Great Pyramid being covered from base to apex with
smooth angular stones. It would indicate that what we witness today is the
original size and shape of the structure.
Recent measures of its
neighbor (P2) indicate its base and upper casing also built on two distinct
ratios of 4/3 (base) and 13/10 (apex).
Returning to P1…
There is an odd feature to
this structure…the 35th course (55.2 Rc above the base).
At this level the stones
measure 2.4 Rc in height and completely out of character with its adjacent
courses of approximately 1.5 Rc high.
It is not logical for the
designers to suddenly change their plans using larger and much heavier stones
for a single layer unless there was a specific reason for its purpose.
Implementing the two vertical
measures from above, an arc of 280.1 Rc in length (calculated height using P1’s
base casing angle) is drawn from the 275 Rc level (calculated from the
present-day upper measurements).
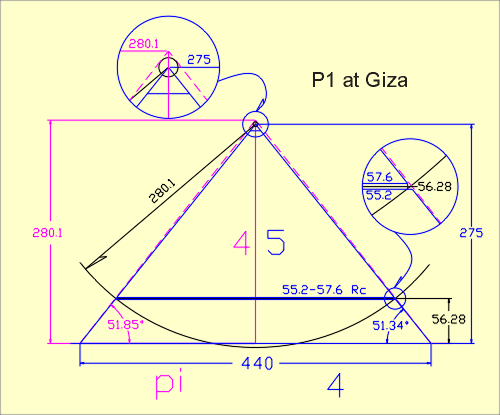
It is noticed that the arc intersects the side of the structure at
the 56.28 Rc level…the exact center of the 35th course!
Was the 35th
course built abnormally high as a marker to confirm the two heights…one
calculated from the base casing and the other from the upper structure’s
measures? Were P1 and P2 designed in a similar fashion, having their upper and
lower angles of different ratios boldly displayed yet easily overlooked for
centuries by the best of surveyors and mathematicians?