The
Second Right-angle Triangle Theory
a2+2a+1 = (a+1)2
Almost two thousand
six hundred years have passed since a young and ambitious mathematician return from
his worldly travels. His voyage had taken him to the northern shores of Africa
where the Nile Delta bestows her spoils into the Mediterranean Sea. Once on
shore he continued his sojourn further south, battling against the rushing flow
of the ever-entwining Nile River. Finally! After several months of weary
travel, he was standing beside the entrance gates of his destination, the gates
leading into the famous Egyptian city…Al-Qahira (Cairo). The goal was to
satisfy his curiosity and quench his thirst for further advancement in the
studies of higher mathematics. The temple priests understood his wanting and
obliged by teaching the mysteries, intricacies, and magic of numbers to this
inquisitive northern traveler. They taught him the geometries and spherical
measures of nature…he discovered and learned…then, upon completion, they
escorted him to the greatest monuments of all time, showing him the perfect
examples displayed in stone…the Giza pyramids. And it is here where he spent
many a-year studying their grand design before retracing his path back toward
home.
But that period of
life had passed…he had now returned to his country and its people…ready and
willing to teach all that he had learned…and so he did. Traveling throughout
the countryside, he was soon to become known as the “Father of Mathematics”,
his name…Pythagoras.
His works included
several revolutionary mathematical concepts and formulae…one being the
“right-angle triangle theory” also known as “The Pythagorean Theorem”.
The most basic
example used to illustrate this mathematical formula is the 3-4-5 triangle and
we have known for centuries that Khafre’s pyramid (P2) at Giza has a sloped
side displaying the identical ratio. Unfortunately, this single ratio was
insufficient evidence to indicate the ancient pyramid builders understanding
the right-angle theory. What must be considered is the possibility of the
builders being completely unaware of the formula; perhaps they had selected
this pyramid slope for another reason (Ill. 1).
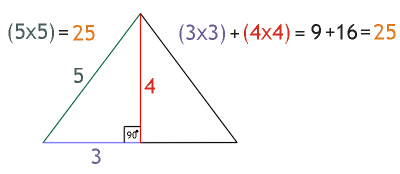
Illustration 1. The 3-4-5 triangle is
designed into Khafre’s pyramid at Giza. This triangle is the most basic example
used to demonstrate the right-angle theory. The sum of the squares of the two
sides equals to the square of the hypotenuse.
The greatest error
was to assume this pyramid side angle being no more than coincidental, that the
ancients did not understand the right-angle triangle theory. Closer examination
indicates the designers actually had complete understanding…greater
understanding than us…the modern intellects we claim to be.
To demonstrate
their knowledge, the builders incorporated other basic integer ratios within
the design. However, these examples were chosen specifically to verify they
knowing of an additional formula for the right-angle triangle (Ill.
2).
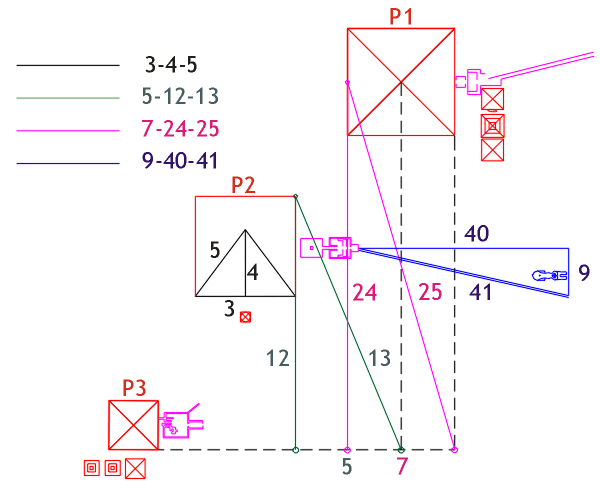
Illustration 2. Hidden within the Giza
complex are several other examples of the right-angle triangle.
Four examples of
the right-angle triangle are illustrated above. The greatest surprise is the
well-preserved causeway on site; it actually forms a 9-40-41 triangle, a ratio
that has never been realized in the past. The four triangles illustrate ratios
of integer values and it is from these examples that a second formula is
developed.
Studying the four
examples it is noticed:
1) The square of the shorter side is equal to
the sum of the other two sides.
2) The hypotenuse has a numerical value one
unit larger than the longer side.
Continuing with the
series…the next example would be 11-60-61. Eleven squared equals 121 and this
value is equal to the total of the other two sides. The hypotenuse is one unit
larger than the other side; therefore it is 61 units, leaving the second side
measuring 60 units.
To arrange this
information into formula context we must begin with the original theory (Ill.
3).
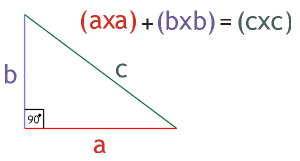
Illustration 3. The formula for the
right-angle theory introduced by Pythagoras.
Using the
Pythagorean theorem for the right-angle triangle and substituting the values as
indicated at the Giza site, only two of the algebraic functions are altered
(Ill. 4).
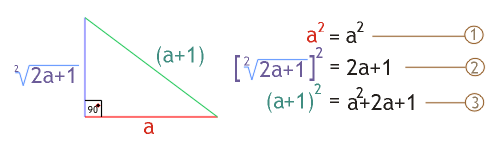
Illustration 4. Substituting the ratios as
demonstrated at Giza for the letters of the right-angle theory and squaring
their sides, line 1 and 2 total and equal line 3.
At first, the
triangle ratios appear complicated, but upon closer examination we realize the
ease in calculation. When the values for a, b, and c are substituted with the
new values then Pythagoras’s formula expands to (a+1)2
= a2+2a+1…one of the many formulas used in basic
algebra.
The system is true…”For
any right-angle triangle having the base measure one unit of length shorter
than the hypotenuse…then the second side of that triangle is the square root of
their sum”.
It is evident that
the formula is ideal for preparing right-angled foundations; also it can be
used for confirming the accuracy of a formed 90 degrees corner. The amazing
advantage is the use of only one value in measure…the three variables: a, b,
and c are now replaced with one measure…“a”. The second advantage of this
formula is the unnecessary calculation of square roots. Below is a simple
example demonstrating the preparation of a right-angle triangle (Ill. 5).
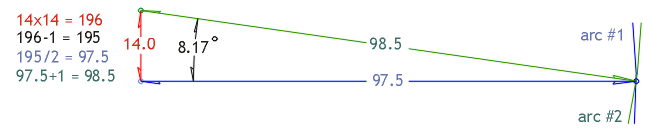
Illustration 5. The calculation and forming
of a right-angle triangle.
To begin: The side
measure of length is selected (example shows 14.0 units). The measure is
squared (14x14 =196). A unit of one (1) is subtracted from the total (196-1 =
195). Dividing this total by two gives the length of the base (195/2 = 97.5).
Add the unit value of one (1) to this measure and it will represent the length
of the hypotenuse (97.5+1 = 98.5). Scribing arcs from both ends of the side
measure will produce the third point of the triangle…the point where the base
and the hypotenuse meet.
The system is not
restricted to integer values; it also applies to decimals or fractions, but
only if the difference of one unit is maintained between the base and the
hypotenuse (Ill. 6).
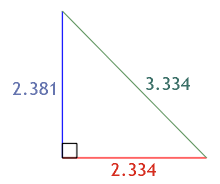
Illustration 6. The formula also applies to
decimal and fractional values, but the one unit difference in measure between
the base and the hypotenuse must be maintained.
For many years
mathematicians have wondered how the ancient Egyptians were capable of
construct their monuments to such accuracy. Amazingly, the bases of these
structures are very close to “true” square. The accuracy in measure certainly
astonished Petrie when recording the dimensions for P1 (Khufu’s pyramid).
The normal
procedure for confirming the 90 degrees corners of a square is to measure the
length of its diagonals; the square is perfect when both diagonals are equal in
length. But, to perform this task, both diagonal paths must be leveled to a
depth equal in height to that of the pyramid’s base corners. Channeling through
rock to level the diagonal strips across the base of the structure, is time
consuming and most impractical. The designers at Giza used the second
right-angle formula to confirm the accuracy of the pyramid corner measures.
They incorporated “squaring” triangles along the pyramid sides and demonstrated
this alignment method in a unique fashion (Ill.7).
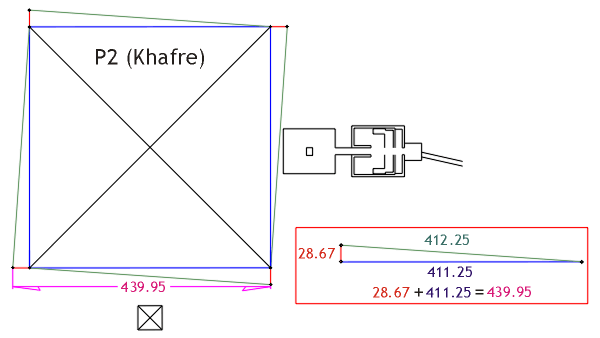
Illustration 7. Squaring triangles used to
confirm 90 degrees corners at the base of P2 (Khufu). The measures are external
to the base boundaries.
Using external
triangles eliminated the problem of leveling the rock along the internal
diagonal lengths. To confirm that the pyramid designers used the second formula
they pre-calculated the width of P2 (Khafre)
plus the extended side measure of the squaring
triangle to equal the width of P1 (Khufu). From above we see that P2 is 411.25 Rc and the side dimension of the squaring
triangle is an additional 28.67 Rc…totaling
439.95 Rc. Khufu’s pyramid side measure is identical…440.0 Rc!
Conclusion:
A second formula for
calculating the side measures of a right angle triangle has been presented.
However, it must be realized that its application is limited to those measures
where the hypotenuses is 1 unit of measure greater than one of the sides. This
formula has the advantage of simple arithmetic calculation compared to the
complexity of square root manipulation. Once the full potential of the formula
is understood, then its application would definitely be favored for determining
and preparing square foundations in construction. The overall dimensions of the
Giza pyramid complex indicated the use of this secondary formula.
Were the pyramid
designers aware of the right-angle triangle theory?
From illustration 2
we learned of the four triangles using integer values in measure. The next in
the series was demonstrated; it would measure as an 11-60-61 triangle; its
calculations were given…now we can witness its location.
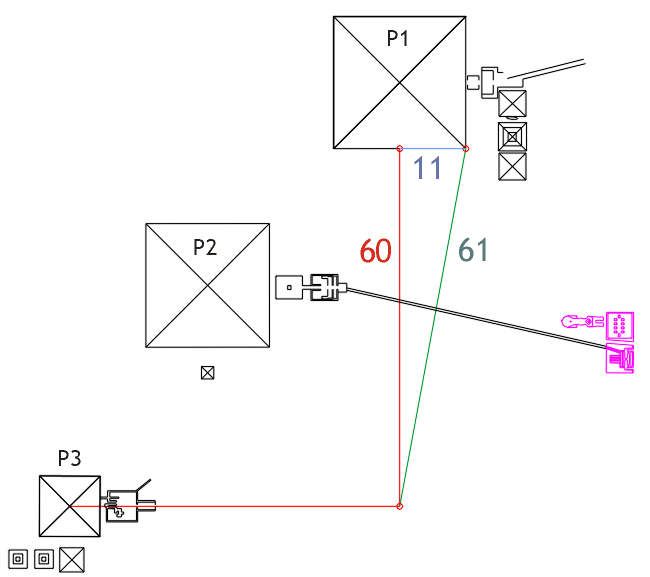
Yes…they did know!
References:
The Pyramids and Temples
of Gizeh…..1882……………Sir W. M. Flinders Petrie
“1o6” The Dawn of
Man………………………….1999 sb……….C. Ross
Clive Ross Amitron2001@yahoo.com