
- From the writings of Book IX:
Having studied ancient Egyptian, Greek, European, and American sites for
twenty years, it has convinced me that our forefathers were fully aware of true
planetary motion. They understood the basics of our solar system and that all
planets, including Earth, orbit the Sun. The evidence collected from many sites
supports my belief and becomes increasingly obvious once their means for
celestial recording are understood.
Although it is against the norm of present-day teachings, the concept of
the ancients understanding astronomy and the inner workings of the heavens must
be weighed with admiration and without bias. It is too easy to overlook and
ignore the simplicity of it all by constantly refusing to use their tools,
their logic, and their means of working hand-in-hand with nature. With all
respect, we must realize their lives and their destiny were controlled by their
beliefs in their gods…the wanderers…the planets.
The science of modern archeology has presented us with an accurate
timetable of events, they are set in place, unable to be adjusted or
manipulated.
The early Greeks learned much from their distant neighbors, the
Egyptians. Unfortunately, during the same historical era, the newly established
democratic state of the Greek republic was bulging from its struggling infancy
stage, a free people…a free voice. But in reality, these were a people
dominated by the religious sector and the influentially power-hungry politika.
New and revolutionary works by philosophers, astronomers, and
mathematicians were well received, but judgment of the material’s content and
validity determined the fate of these same individuals. The Pythagoreans were
no exception; in fact, they became the example.
Pythagoras had personally rejected a fellow citizen named Cylon who had
great ambitions of joining the Pythagorean society. It was felt his character
unfitting; he did not meet the standards set by the founder. In retaliation,
Cylon venomously incited the persecution of 508 BCE and the final demise of the
Pythagoreans. It is believed that Pythagoras escaped the “cleansing”, fleeing
to Metapontium where he continued his work until his final days.
To avoid detection and a possible repeated massacre, the forbidden
Pythagoreans regrouped and developed a means of communicating and recording of
their findings in coded format. The system was similar to Plato’s writing style
with the addition of numerical values scattered throughout the writings. This
great philosopher had publicly proclaimed his personal success on its use. It
was the ability to write a primary story and hide it within the writings of one
or more secondary yet insignificant stories, in a manner so unique that only
those with full understanding could detect its presence.
More than four hundred years had passed since that harrowing event with Cylon,
when an aging and renowned architect/mathematician/astronomer named Marcus
Vitruvius Pollio composed a collection of works titled “Ten Books on
Architecture”.
The ten books explain in great detail the mathematical and intricate
methods for constructing the finest of monuments and buildings. Miraculously
the collection survived and was successfully translated from Latin, yet within
the writings of book IX, relating to planet motion, there remain the mysteries
and the conjuring of unrealistic numbers presented by the author.
As an architect, Vitruvius was a genius. As an astronomer, it appears he
was a dismal failure. But perhaps he was a follower of the Pythagoreans with
the writing skills of Plato; will we ever know?
If true, then a primary story may be locked within the confusion of his
writings, a story that has avoided detection for more than two millennia?
From the writings of Book IX:
There are ten books in total, each relating to an individual
topic. All books begin with an introduction of the topic in question followed
by short explanatory chapters. However, this paper focuses on book
IX “…the whole system of nature together with the
firmament and its stars…” Vitruvius IX, specifically the contents and examples in the introduction compared to
the information provided in the chapter that follows.
The reader is reminded of “…the doctrines of Pythagoras, Democritus,
Plato, Aristotle, and other sages…” and how their individual accomplishments
have benefited society. Examples of
their work are testament to their everlasting fame in the science of
mathematics. They are as stated:
1)
Demonstrated to Plato: What length of side is measured for a square
having an area equaling 200 square units. It cannot be fifteen, since fifteen
times fifteen equals two hundred and twenty five. Nor can it be fourteen, since
fourteen times fourteen equals one hundred and sixty nine. The number lies
between both “…we cannot find them by the aid of numbers…”. However, it is
explained that it can be achieved using geometry, it was first demonstrated by
Pythagoras and the simple diagonal measure of a square (Ill. 1).
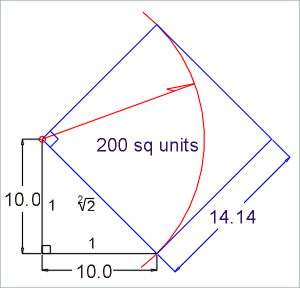
Illustration
1. With the aid of instruments,
Pythagoras illustrated how a right-angle triangle is used to calculate a side
measure of a square containing 200 units.
2)
Pythagoras demonstrated his theory of forming a right-angle triangle
using a formula relating to the square. The square of the hypotenuse equals the
sum of the squares of the other two sides. “…When Pythagoras discovered this
property, convinced that the Muses had assisted him in the discovery, he
evinced this gratitude to them by sacrifice…” (Ill. 2)
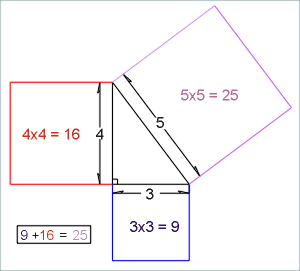
Illustration 2.
Pythagoras developed the right-angle triangle theory without the aid of
instruments.
3)
Of Archimedes “…He then placed the mass of gold in the vessel…found that
the water which ran over was lessened…as the magnitude of the gold mass was
smaller than that containing the same weight of silver. After again filling the
vase by measure, he put the crown itself in, and discovered that more water ran
over then than with the mass of gold that was equal to it in weight…he found,
by calculation, the quantity of silver mixed with the gold, and made manifest
the fraud of the manufacturer…”
4)
“…From Archytas the Tarentine, and Eratosthenes of Cyrene we are
credited with the means of satisfying the response of Apollo of Delos, which
required an altar to be made similar to his, but to contain double the number
of cube feet…” (Ill. 3).
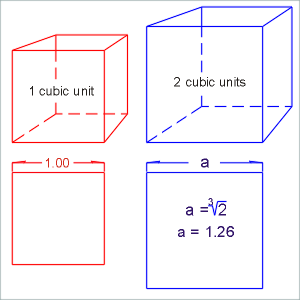
Illustration 3.
Solving the problem of two cubes. The challenge was to create an altar
containing double the volume of Apollo’s altar.
Vitruvius composed an intriguing introduction for a book dedicated to
astronomy. It delves into the mathematical problems and scientific
accomplishments by those of past fame without any reference to the main
objective of this chapter, the teachings of the heavens above. Most puzzling.
Note: We must consider the difficult task of the translator to correctly
assume the author’s intentions especially if he or she is not familiar with
astronomy. Expression of thought may differ from that of the author but
numerical values remain unchanged.
It is the first chapter where confusion is encountered between
Vitruvius’ data and true planetary measures.
1)
We are informed that the Sun, Moon, Mars, Jupiter, and Saturn orbit
Earth while Mercury and Venus orbit the Sun. This “geocentric” (Earth center)
theory was first introduced by the Greek astronomer Aristotle (384-322 BCE)
(Ill. 4).

Illustration
4 The geocentric cosmos with the outer
twelve zodiacs (constellations) as proposed by Aristotle.
This concept of the heavens was their standard teaching and strictly
enforced by the religious sector, but unaccepted by the Pythagoreans.
The reason?
Astronomers had learned much since
Aristotle’s time; his center-Earth theory had many downfalls. Following his
death, the famous astronomer Aristarchus of Samos (320-250 BCE) presented a
less complicated scenario. He disagreed with Aristotle’s teachings and
theorized that Earth and the other planets were in motion around the central
Sun. It was the first suggested theory indicating that all planets orbited the
Sun; the “heliocentric” system introduced by an individual born two hundred
years before the writings of Vitruvius! The religious establishment rejected
this radical concept and remained in favor (enforced) Aristotle's geocentric
system.
Irrelevant of which theory was correct, Vitruvius ensured or
attempting to pacify his readers that he was a follower of Aristotle’s
teachings. It was mandatory; it allowed him the freedom to enter the numbers he
required to entwine his primary story within the writings and for his books to survive.
2)
The writings continue and Vitruvius enters his inconsistent planetary
data:
a)
The Moon orbits Earth in synchronization with the Sun. It has a sidereal
cycle (measure not given) and completes thirteen intervals of 28 days and 1
hour during one transit of the Sun through the heavens. The total cycle
would be (13 x [28 days and 1 hour]) = 364.52 days…not mentioned.
b)
Mercury, the planet closest to the Sun, completes one cycle in 360 days,
passing through the 12 zodiacs, spending 30 days in each.
c)
Venus, the second closest planet to the Sun, completes one cycle in 485
days; it passes through each zodiac in 40 days.
d)
One Mars cycle is 683 days in length. It must be noted: There is no
mention of the number of days Mars remains in each zodiac.
e)
Jupiter’s cycle is much longer, totaling 11 years and 323 days; it
remains in each zodiac for a period of 360 days.
f)
Saturn requires the longest to complete one cycle, totaling 29 years and
160 days. We are informed that it is equivalent to 31 months in each of the 12
zodiacs.
The information given has too many basic errors. It invites the
inquisitive astronomer to compare the numbers to the actual days for these
celestial objects to complete their orbits (Data 1).
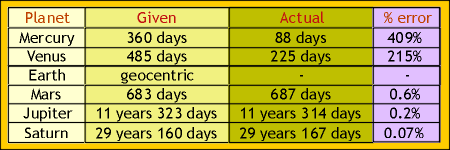
Data 1. Planetary
data as recorded by Vitruvius compared to their actual orbital period; included
is the percentage error.
3)
Following the planetary data, Vitruvius adds another passage of
interest:
“…Thus, on a wheel similar to those in use among
potters, if seven ants be placed in as many channels round the center, which
are necessarily greater in proportion to their distance there-from, and the
ants are forced to make their circuits in these channels, whilst the wheel
moves round in an opposite direction, they will assuredly complete their
circuit, notwithstanding the contrary motion of the wheel; and, moreover, that
nearest the center will perform his journey sooner than he who is traveling in
the outer channel of the wheel, who, though he move with great velocity, yet,
from the greater extent of is circuit, will require a longer time for its
completion. It is even so with the planets…”(Ill. 5).
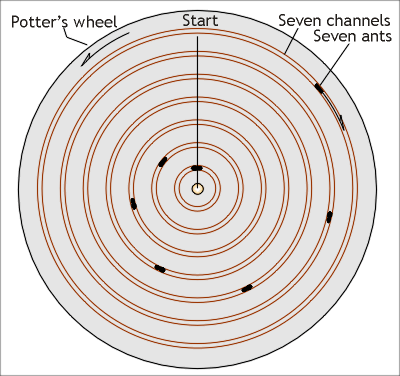
Illustration
5. Seven ants in seven channels
marching in the opposite direction of the potter’s wheel.
a)
Is the author indicating to the reader that he actually believes all
planets orbit the Sun; not Earth?
b)
If he were suggesting Aristotle’s Earth-center concept then two ants,
representing Mercury and Venus, would be circling around a single ant
representing the Sun in its own channel; this is not the case. Therefore his
writings could be indicating his rejection of Aristotle’s theory in favor of
the heliocentric system proposed by Aristarchus.
c)
Do the seven ants represent the Moon plus the six planets: Mercury,
Venus, Earth, Mars, Jupiter, and Saturn orbiting the Sun, or do they exclude
the Moon since its orbit around Earth was an established fact?
d)
Could Vitruvius have been suggesting that an additional planet existed?
Do the seven slow moving ants represent seven planets? Is it possible that he
was referring to the Greek’s wandering mythical god Ouranos (Uranus), the
father of Cronus (Saturn), the next planet from the Sun after Saturn?
There are speculations suggesting that Uranus was known to the ancients
but only observed by a select few, those with excellent eyesight. Visible or
not, it was impossible to confirm that Uranus actually existed until its discovery
in 1781 by William Herschel with the aid of his home-built telescope. Until
that time the planet could only be observed occasionally by the naked eye in
clear skies appearing as a dim and almost stationary star, not the obvious glow
of our closer and faster moving planets.
To strengthen the concept there are the myths that explain:
“…Very far, very far, right at the furthest end of
the dome of heaven (Ouranos)…"-Aristophanes Peace 499
“…But when she was about to bear Zeus, the father
of gods and men, then she besought her own dear parents, Gaia and starry
Ouranos,…” -Theogony 459-478
Perhaps the planet Uranus (Ouranos) is something to be considered and
not overlooked.
Vitruvius presents a large amount of information within a small space of
text. He certainly knew his architecture, histories, sciences, and astronomy,
but did others?
To the layperson all data appeared genuine and in perfect order,
fortunately these were not dedicated and knowledgeable astronomers. Vitruvius was
an avid astronomer, spending countless evenings dedicated to observing and
monitoring the “wanderers”; the ancients’ most recognized gods. He understood
planet motion in great detail, allowing him to gamble on his peers’ ignorance
and the opportunity to encode his findings within the texts.
Vitruvius informs the reader of Mercury and Venus orbiting the Sun and
it is immediately obvious that the measures for these two planets are
completely over-exaggerated. It is unimaginable how he could dare offer these
measures as true. Mercury is closest to the Sun and difficult to observe for most
of its orbit, completing four orbits in one year, yet we are told it requires
360 days, far from the actual 88 days. The measure for Venus is also difficult
to realize. The 485 days suggested is more than double the true measure of 225
days. However, Venus and Earth have a synodic (realignment) period of 584 days,
and it should be noted that the numbers he enters (485) are correct but in
reverse order.
The most staggering error is the thirteen Moon circuits of 28 days and 1
hour for one Sun cycle. Not only is the one-hour accuracy irrelevant in the
presentation, but it also produces two incorrect measures!
a)
Thirteen Moons of 28 days and 1 hour are equivalent to 364.52 days and
we are aware that astronomers knew the Earth/Sun cycle of 365 ¼ days. How could
Vitruvius calculate the year cycle using an incorrect value for the Moon’s
period, yet calculate Saturn’s orbit to such accuracy using the same object…the
Moon?
b)
The Moon is closest to Earth and its motion studied for millennia;
astronomers knew the period for a single Moon cycle to the second. Using
Vitruvius’ measure and calculating in reverse, the sidereal period would be
27.26 days (actual 27.32 days), more than one hour short of true measure, yet
the man stipulates his measure accurate within the hour. It is not possible to
calculate an error of this magnitude.
The pattern is forming, the signs are there, and the mistakes most
evident, but only to those having knowledge in the field of astronomy. His
outer planet measures are exceptionally accurate and it is this accuracy
coupled with the gross inaccuracy of measures for the Moon, Mercury, and Venus
that indicate the possibility of intentional numerical errors. There is no
other logical explanation. Leaving us with the questions…was it intentional,
why did he do it, and can it be proven?
The author was fearless of reprisal for his work. The inconsistent data
of Book IX, relating to astronomy, would be investigated closely but not taken
seriously. Heads would shake, some would chuckle, his work disregarded and the
author ridiculed. Amazingly…that is exactly what occurred.
Before analyzing the numbers, it must be realized that mathematics in
the days of Vitruvius was a means of occupying one’s spare time. It stimulated
the power of reasoning while feeding the starved and ever-curious mind.
Surprising perhaps, but it was a game played without the use of written words.
Numbers were manipulated, transferred, reversed, cross-multiplied, and divided
in replacement of normal functions. For some it was more; it was a challenge to
improve calculation systems and the further advancement of formulae; these were
the true Pythagoreans. However, the constant fear of exposure and reprisal by
the bureaucracy made their plight exceedingly difficult. Understanding their
situation and placing oneself in the position of the author is mandatory. It
allows the reader to focus on the information presented and the choice of tools
required to separate the truths from the untruths.
The numbers and ratios to follow are extracted from the contents
provided, and it must be emphasized that a multitude of trial and error
calculations were required to uncover these results. The hand-held calculator
is a wonderful tool; had these calculations been attempted using the Roman
numeral system then all that is hidden would have never been realized.
An example:
485 x 485 = 235,225
It is a long and tedious mathematical task using Roman numerals to
calculate the answer, increasing the probability of error:
![]() CDLXXXV x CDLXXXV
= ccxxxvCCXXV (over-lined letters denotes 235 multiples of 1000).
CDLXXXV x CDLXXXV
= ccxxxvCCXXV (over-lined letters denotes 235 multiples of 1000).
1.
Vitruvius’ introduction begins with an irrational number
problem, explaining that the square root of two could not be calculated. But it
must be realized that he elected to use the number 200 not 2.
Although he states the problem unsolvable (offers
15 x 15 and 14 x 14) he does explain how to attain the correct value by simply
extending the number to be squared by a multiple of 100 (2 x100 = 200).
Increasing the number by another multiple of 100 to 20,000 would result in an
answer between 141 and 142, much closer to the true value of 1.414. Therefore it
is a fact that he knew how to calculate the answer by approaching the problem
from the opposite direction. To confirm, he presents the planet Mars orbiting
in 683 days while Venus requires 485 days and it is obvious that the days for
Venus are drastically incorrect. Since Vitruvius compared the Moon cycle to
that of the Sun then he must have compared Venus to Mars. This would result in
a ratio of 683/485…or 1.41:1…and amazingly…the square root of two…the answer to
the initial problem…the same problem that couldn’t be resolved using numbers!
Note: Vitruvius claims that Mars orbits the Sun in 683 days (actual 687),
yet his calculations for the distant planets: Jupiter and Saturn are very
accurate.
Dividing his 683 by the square root of two, then the actual answer is 483…not
the 485 as shown above. The result produces the perfect answer with an additional
feature. The difference between values (683-483) equals 200, and it is a
200-unit square he selects to present the original mathematical dilemma.
Was he aware of the 683:483 combination, did he begin with these numbers
then sacrifice the opportunity to demonstrate his mathematical skills to accommodate
for more important calculations? It would certainly explain why the error of
days for Mars is high (Ill. 6).
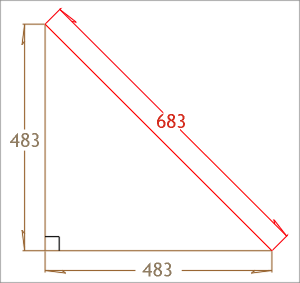
Illustration 6.
Vitruvius fails to demonstrate the perfect 683/483 right-angle triangle where the
difference in values is 200 units, indicating both numbers being significant
for other calculations.
2)
There was an ulterior motive for selecting the 200 units; it is boldly
presented in his first numerical attempt to calculate the square root of 200.
[“…It cannot be fifteen, since fifteen times fifteen equals two hundred and
twenty five…”]. Venus orbits the Sun in 225 days. How very simple! A perfect
example demonstrating how numbers from an irrelevant statement direct the
reader to facts relating to astronomy, the primary reason for writing Book IX.
The 225-day orbit for Venus is acknowledged and
this perfect count can be compared to the 485 days that Vitruvius elected to
use. The count is greater than the true measure by 260 days (485-225 = 260), and
260 was a significant number for ancient astronomers. Investigating further and
substituting Earth days for Venus days the answer is 120 days (485-365 = 120) and
this definitely confirms why the 485 count was necessary. Two numbers: 260 and
120 can only refer to Earth and Mars (Data 2).
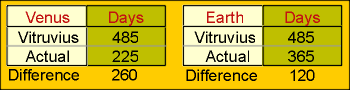
Data 2. Day count for Earth and Venus subtracted
from the 485 value entered by Vitruvius.
Used also by the Aztecs, the 260-day calendar
system will see Earth travel 120 degrees further ahead of Mars in orbit. Three
sets of 260 days equals 780 days, completing the time required for Earth to
catch up and realign with Mars…the synodic period for Earth and Mars (Ill. 7).
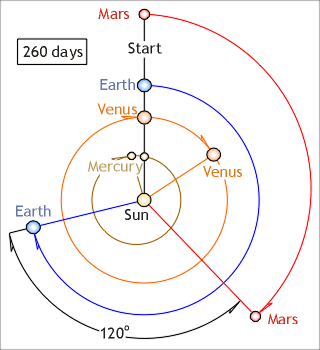
Illustration 7.
The 260-day Aztec calendar uses the Earth-Mars synodic period. Earth travels
120 degrees further in orbit after 260 days and realigns with Mars in (3 x 260
days) = 780 days.
3)
Vitruvius had to confirm his numbers correct for them to fit within a
larger scheme than first anticipated. They had to be altered slightly to
satisfy his purpose and prove his choice intentional. The simple
addition-subtraction of three numbers for Mercury, Mars, and Jupiter confirm
the obvious (Data 3).
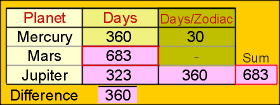
Data 3. Comparing
the sum and difference of data from Mercury, Mars, and Jupiter indicates the
number 323 being relevant.
4)
The author could not resist the opportunity to demonstrate the classical
right-angle theory. His admiration and respect for the mathematicians of old is
overwhelming and a tribute is made to Pythagoras the “Father of Mathematics”.
Using the information from Data 1, it is discovered that the square of 360
(days for Mercury) is equal to the sum of the squares of 323 (days for Jupiter)
and 160 (days for Saturn) (Ill. 7).
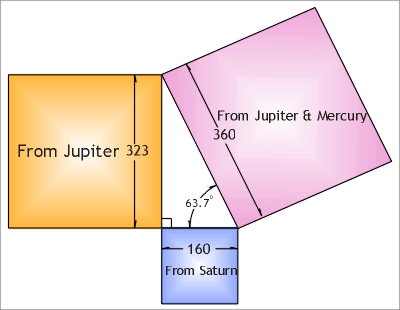
Illustration
7. Data from the planets: Mercury,
Jupiter, and Saturn are used to demonstrate the right-angle triangle theory.
5)
There is one superb example of numerical manipulation illustrating the
mathematical ability of the Pythagoreans, and Vitruvius offers his planetary
data to illustrate their brilliance. The time periods he gives for Venus and
Mars could have been reduced further to show years and days; Venus orbits in 1
year 120 days, not 485 days given; Mars orbits in 1 year 318 days, not 683
days. This would change the column totals to 42 years 1281 days. The day numbers
are then reversed producing a completely new set of numbers, yet their total remains
equal in value (Data 4)!

Data 4. A
remarkable display of numerical manipulation to create two columns of reverse
values having equal totals.
6)
The following are two important steps; they must be fully realized and
not confused with the ambiguity of the written text
a)
The only information Vitruvius presents for Mars is the 683-day orbit
period, four days short from the perfect 687-day count. He excludes the time
the planet spends in each zodiac. From true measure the average is 57 days
(687/12).
b)
Second to this small oversight is the confusing count of days for Saturn
in each zodiac. Vitruvius diverted from day count to month count, stating 31
months for Saturn in each zodiac.
A Sun cycle equals thirteen Moon counts of 28 days
and 1 hour, but this day count is not the actual sidereal measure insinuated by
the author. As previously presented, Vitruvius conveniently omitted the true
measure in his writings; the sidereal month is 27.32 days. Therefore the total
period that Saturn remains in each zodiac equals (31 x 27.32 days) = 847.54
days. The measures for all objects in each zodiac are now converted using days
only (Data 5).
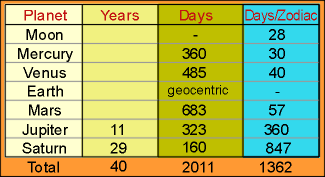
Data 5. The final column completed showing the
average days for each planet to pass through a single zodiac sign.
7)
Comparing the total days from Data 5 produces a ratio of 1362/2011 =
0.677:1. This ratio is equal to the synodic period for Saturn with Jupiter, the
furthest two planets visible without the aid of magnification. On average,
Jupiter will realign every 0.674 orbits of Saturn or 242.3 degrees. The
difference between the true ratio measure and that from Data 5 is small.
However, it must be remembered that the error in orbital periods given by
Vitruvius for these two planets is also small (Ill. 7).
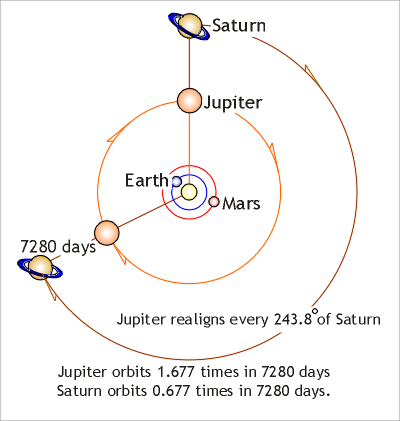
Illustration
7. From Vitruvius’ measures Jupiter and
Saturn realign (synodic period) every 0.677 orbits of Saturn or 7280 days
(actual alignment is every 7252 days).
While confirming these values, an unprecedented
accuracy in measure was discovered.
From Vitruvius: Saturn orbits in (29y + 160d) =
10,752 days, Jupiter in (11y + 323d) = 4,341 days. The alignment ratio is the
orbital period of Jupiter (4,341 days) divided by the difference between both
periods [(10,752 - 4,341) = 6,411 days] = 4,341/6,411 = 0.677:1.
Comparing this ratio to the ratio of the two totals
of day count from Data 5 (2011/1362) = 0.677:1. They are identical ratio!
What Vitruvius is presenting is the comparison of
orbital ratios for two planets: Jupiter and Saturn being identical to the ratio
of the addition of total planet days compared to the addition of total zodiac
days, and two zodiac measures did not exist, they were left for the reader to
calculate. Three completely different entities are used to produce two
identical ratios. Further examination reveals that a small and intentional
adjustment was made to the Jupiter and Saturn orbital periods to accommodate
for the mathematical features already discussed.
The actual number of days for Jupiter and Saturn to
orbit the Sun is 15,092 days (10,760 + 4,332 = 15,092 days); Vitruvius offers
15,093 days (10,752 + 4,341 days = 15,093 days), within one single day of
accuracy. His increasing the orbital period for Jupiter and decreasing the
period for Saturn allowed him to manipulate the planetary data to demonstrate
the formulas presented in his introduction…a truly remarkable feat!
8)
With most information in place there is one final stumbling block, the
number of days for Mercury to orbit the Sun. Why did Vitruvius suggest 360 days
when it only requires 88 days? This over-exaggerated value is there for one
purpose, to increase the total count of days.
Adding all data for the planets the total equals 40
years and 2011 days (Data 5). The days are converted to years producing a new
total of 45.5 Earth years and it is here where the main story is discovered
deep within the numbers.
The planets and their orbital characteristics have
been discussed, but according to Greek legends, Saturn had a
father…Ouranus/Uranus…the seventh planet from the Sun. Uranus requires 84.02
Earth years to complete one orbit of the Sun; during this interval Saturn will
orbit 2.85 times. These two planets have a synodic period of 1.54 orbits of
Saturn; the two planets realign every 45.4 years (1.54 x (29 years 167 days)).
By the most remarkable mathematical coincidence
Saturn and Uranus have a synodic period of 45.4 years, a mere fraction of an
Earth year from the 45.5 years total provided by Vitruvius for all planets (Ill
8).
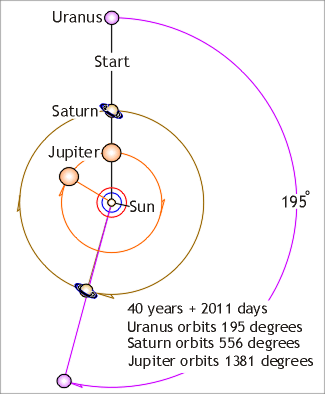
Illustration 8.
The two planets: Saturn and Uranus align in the same time as the total for all
planets given by Vitruvius
Comparing the most accurate measure from NASA, the
difference between modern measures and those by Vitruvius is 51 days from a
total count of 16,621 days, an error of only 0.3%.
It appears impossible for the ancients to have
known the orbital relationship between Uranus and Saturn, but Vitruvius
confirms his findings toward the end of the book by describing several unique
details. He had to; it was his only means of directing the reader toward the
evidence, and it was necessary to prove his calculations intentional.
From Chapter 4:
“…Above
Sagittarius, Scorpio, and Libra, comes the Serpent, the point of whose snout
touches the Crown…”
[…The “crown” represents Archimedes problem of gold
being replaced with silver. Vitruvius replaced true planetary data with
falsified information…]
From Chapter 5:
“…First, under
Capricornus is the southern Fish looking towards the tail of the whale. Between
it and Sagittarius is a vacant space. The Altar is under the sting of Scorpio…”
[…Doubling of the cube of the “altar” represents the
double/two meanings for the data entered and the ingenious manipulation of numbers
to form complicated ratios relating to planetary motion…]
From Chapter 8:
“…The hole being lowered through the space of
Scorpio and Sagittarius…”
[…The “hole” is what had to be discovered; the
place where all flows into. It directed us to the truth and real purpose for
his work…]
These three pieces of text share one common
element…they all refer to the zodiacs: Sagittarius and Scorpio.
Vitruvius completed his ten books on architecture
approximately 30 BCE. During that year, Saturn aligned with Alnilam, the center
star of Orion’s belt. At that same moment, Uranus entered into the abyss of
cosmic clouds between the zodiacs: Scorpio and Sagittarius…the “hole” marks
that very location.
Vitruvius introduced the ninth book of astronomy into his works, making
the greatest of error by claiming the Moon’s orbit is in harmony with the Sun
having a cycle equal to 28 days and 1 hour. Yet it was common knowledge to most
astronomers that the Moon had a cycle less than 28 days. The hour added was an
irrelevant measure, yet it is the key word that sparks the interest of those
who study mathematics and astronomy.
Mercury can be observed with ease; approximately every 115 days when it
can be found in the same location with respect to the Sun. But its orbital
period is less, only 88 days, not the over-exaggerated 360 days stated.
Pythagoras was the first Greek who claimed that Venus orbited the Sun,
it is the brightest and most adorned of all planets with a cycle of 225
days…not the 485 days proposed.
The omission of days allocated to the zodiac period for Mars and the use
of months to express Saturn’s term in each zodiac instigated the calculation of
days for every planet, producing the required information to complete the
latter segment of this book on mathematics relating to astronomy.
Coincidence perhaps, but did the seven ants in the seven channels
represent the seven years that the seventh planet Uranus spends in each of the
zodiacs (7 years x 12 zodiacs = 84 years total). This planet may have been
known to exist at the time of the writings, but only observed by those blessed
with perfect vision. Knowledge of its motion could never be ascertained with
certainty until the invention of the telescope.
The author understood the motion of all planets and their timely path
around the Sun. Then meticulously he set out to credit those before him, for
their dedicated efforts and contributions to science. He risked being exposed
in a daring manner, constantly facing the possibility of death or imprisonment.
His works were not designed for his time but for those of his future…for us, to
gain a clearer understanding of the heavens and its cosmic elements that
controlled his, and now our very existence and destiny.
After two millennia, Vitruvius the Pythagorean finally succeeded!
Book IX of “De Architectura Libri Decem” …Marcos Vitruvius Pollio (c.
90-20 BCE).
Translated from the Latin by Joseph Gwilt, London, John Weale, 1860
See Book
IX reference Bill Thayer.
In The Beginning
http://www.varchive.org/itb/uranus.htm …Imanuel Velikovsky
See Uranus
The Giza Pyramids …2001 …Clive Ross
See all
topics
Larousse Astronomy …1986 …Philippe de la Cotardiere
“1o6” The Dawn of Man …1999 …Clive Ross
Planetary data …NASA
See Planets
_______